Esta Política de Privacidade (“Política”) integra os Termos de Uso do site do Por Quê? (“PQ?” ou “Site”), sendo-lhe aplicável todas as condições dos Termos. Esta Política vincula o usuário que acessar ou utilizar o PQ? (“Usuário”) e a Bei Comunicação Ltda. (“Bei”).
1. Informações Coletadas
1.1. O PQ? coleta dados relativos ao seu acesso e uso do Site, de forma anônima caso o Usuário não tenha iniciado uma sessão identificada por meio de conta do Site (“Dados Não Identificados”). Os Dados Não Identificados compreendem:
(a) registros de navegação (logs), como endereço IP, data e hora de início de acesso, data e hora de encerramento de acesso, entre outros;
(b) cookies, que são mecanismos de monitoramento de atividades em sites, que indicam para a Bei os seguintes dados sobre o navegador utilizado para acessar o PQ? e sobre o acesso feito pelo Usuário no site: (i) idioma; (ii) país, estado e cidade; (iii) navegador, sistema operacional e provedor de serviços de Internet; (iv) resolução de tela, tipo de dispositivo (desktop, tablet ou smartphone), modelo do aparelho do dispositivo; (v) páginas e Conteúdos do PQ? navegados pelo Usuário; (vi) se o Usuário está naquele momento navegando no Site; (vii) tempo de navegação no Site; (viii) se o Usuário acessou o Site através de um mecanismo de busca (p.ex., Google, Bing) e termo de pesquisa que utilizou para acessar o Site ou se acessou o Site diretamente por meio do domínio porque.com.br ou porque.uol.com.br; (ix) interesses do Usuário como, por exemplo, afinidades ("notícias e políticas", "esportes e fitness", "compras", "estilo de vida e hobbies") e segmentos de mercado ("educação / ensino pós-secundário", "emprego", "educação / preparação para teste e tutoria", "emprego / governo e emprego no setor público", "viagens / viagens aéreas").
1.2. Caso o Usuário deseje desabilitar o monitoramento via cookies, basta recusar seu uso na caixa de diálogo que aparece na parte inferior do Site, quando do primeiro acesso, ou no link Uso de Cookies constante do rodapé do Site.
1.3. Adicionalmente aos Dados Não Identificados, o PQ? poderá solicitar ao Usuário os seguintes dados pessoais (“Dados Identificados”):
(a) nome completo;
(b) número de inscrição do Usuário no Cadastro da Pessoa Física (CPF);
(c) número de celular;
(d) endereço de e-mail;
(e) CEP, logradouro, complemento, Município, Estado e país de residência;
(f) data de nascimento ou idade;
(g) gênero indicado no documento de identidade, sem vinculação à vida sexual do Usuário;
(h) nível de escolaridade;
(i) profissão ou ocupação;
(j) situação atual de trabalho;
(k) rendimento familiar mensal;
(l) se o usuário possui conta em banco;
(m) se o usuário possui cartão de crédito.
1.4. O fornecimento dos Dados Identificados ficará a critério exclusivo do Usuário, mas algumas funcionalidades do PQ? poderão estar disponíveis apenas a usuários que prestem determinados Dados Identificados.
2. Uso das Informações
2.1. O PQ? coleta, armazena e trata os Dados Não Identificados para (a) melhorar a experiência do Usuário no uso de nossos canais de comunicação (incluindo redes sociais e este Site) e dos Conteúdos e (b) realizar estudos acadêmicos, em parceria com professores e instituições de ensino, para aprimorar o estudo da economia.
2.2. O PQ? coleta, armazena e trata Dados Identificados para a finalidade especificada na cláusula 2.1 e para contatar e interagir com os Usuários por meio de newsletter, redes sociais, e-mail, aplicativos para dispositivos móveis, como Whatsapp, por exemplo, e outros canais de comunicação usados pelo PQ?.
2.3. Observadas as finalidades previstas nas cláusulas 2.1 e 2.2, a Bei poderá tratar Dados Não Identificados e os Dados Identificados (conjuntamente referidos como “Dados”) de forma a:
(a) confirmar a identidade do Usuário para futuros contatos e aprimoramento de sua experiência no Site;
(b) contatar e interagir com os Usuários;
(c) criar cópias de salvaguarda (backup) dos Dados;
(d) analisar tráfego, ações, campanhas e outras informações obtidas a partir dos Dados;
(e) gerar estudos estatísticos e de outra ordem a partir dos Dados para uso pelo PQ? e para fins acadêmicos;
(f) promover Conteúdos e eventuais serviços ofertados via Site;
(g) aperfeiçoar a navegação, funcionalidades e Conteúdos do Site, assim como a interação dos Usuários com newsletter, redes sociais, e-mail, aplicativos para dispositivos móveis e outros canais de comunicação usados pelo PQ?;
(h) criação de serviços, novas funcionalidades, aplicativos, ferramentas e derivações do Site;
(i) defender interesses e exercer regularmente direitos em processo judicial, administrativo ou arbitral;
(j) verificação do cumprimento dos Termos de Uso do PQ?, demais regramentos do Site e da legislação vigente, quando aplicável.
2.4. O Usuário declara-se ciente de que a Bei poderá disponibilizar e revelar os Dados Não Identificados e os Dados Identificados (conjuntamente referidos simplesmente como “Dados”) para autoridades públicas, em cumprimento da legislação vigente ou de eventual ordem judicial ou de autoridade competente.
3. Armazenamento, Acesso e Segurança
3.1. A Bei poderá armazenar e tratar os Dados em datacenter no Brasil ou no exterior, próprio ou de terceiros. Neste último caso, os fornecedores deverão cumprir o disposto nesta Política quanto ao tratamento dos Dados. Na hipótese de transferência internacional dos Dados para tratamento no exterior, o fornecedor e o país de destino deverão cumprir com a legislação brasileira vigente.
3.2. Atualmente, os Dados são armazenados e tratados nos Estados Unidos da América, por prestador cujos serviços estão em conformidade com o GDPR – General Data Protection Regulation, norma da União Europeia que regula o tratamento de dados pessoais.
3.3. Os Dados poderão ser acessados apenas por profissionais, contratados e parceiros da Bei que necessitem tratá-los para os fins e nos limites desta Política e que cumpram o disposto nesta Política.
3.4. O Site e os Dados contam com os seguintes mecanismos de segurança:
(a) SSL – Secure Sockets Layer: tecnologia utilizada para a segurança na comunicação entre o Usuário e o Site;
(b) Criptografia: os bancos contêm os Dados, a imagem do sistema operacional que hospeda o Site e os backups do Site e dos bancos de dados são protegidos por criptografia. Essa tecnologia torna ininteligível as informações por ela protegidas, permitindo que apenas o detentor de uma chave consiga reverter o processo;
(c) WAF – Web Application Firewall: camada de segurança que protege de invasores o Site e seus recursos de software;
(d) Backup: sistema automático que salvaguarda diariamente o Site e os Dados por 30 dias;
(e) Security Groups: sistema que isola o banco dos Dados de acesso direto à Internet, só sendo acessível através dos aplicativos que compõem o Site;
(f) Firewall na VPC – Virtual Private Cloud: sistema que funciona como uma barreira virtual, abrindo e fechando portas de acesso aos aplicativos do Site para a Internet, limitando as oportunidades de invasão.
3.5. O PQ? é submetido periodicamente a testes de invasão, a fim de identificar no sistema pontos de vulnerabilidades para serem corrigidos e solucionados.
3.6. Além das medidas previstas nesta seção, a Bei poderá adotar outros mecanismos de segurança para incrementar as barreiras ao acesso não autorizado a Dados e ataques ao Site.
4. Direitos do Usuário
O Usuário, a qualquer momento e mediante requisição, poderá demandar quanto a seus dados pessoais:
(a) confirmação da existência de tratamento;
(b) acesso aos seus dados;
(c) correção de dados incompletos, inexatos ou desatualizados;
(d) anonimização, bloqueio ou eliminação de dados desnecessários, excessivos ou tratados em desconformidade com o disposto nesta Política ou na legislação vigente;
(e) eliminação dos dados pessoais tratados com o consentimento do titular, exceto nas hipóteses previstas em lei e conforme necessários para o cumprimento de obrigações legais ou para defesa dos interesses da Bei;
(f) identificação das entidades públicas e privadas com as quais a Bei compartilhou dados;
(g) revogação do consentimento para usos posteriores, permanecendo válidos e lícitos os usos regulares já realizados.
5. Glossário
As palavras e expressões relacionadas abaixo, quando utilizadas nesta Político, terão os seguintes significados:
Backup: mecanismo de salvaguarda dos Dados e dos recursos de software do Site.
Controlador: Bei Comunicação Ltda., titular do PQ? e das bases compreendendo os Dados.
Cookies: mecanismo de monitoramento de atividades do Usuário no Site (p.ex., páginas do PQ? visitadas, Conteúdo acessado), provendo ao PQ? as informações referidas na cláusula 1.1(b) desta Política.
Criptografia: tecnologia torna ininteligível as informações por ela protegidas, permitindo que apenas o detentor de uma chave consiga reverter o processo.
Dados Identificados: são os dados relacionados na cláusula 1.3.
Dados Não Identificados: são os dados relacionados na cláusula 1.1.
Dados: conjunto de Dados Identificados e Dados Não Identificados.
Endereço IP: identificação do provedor de Internet ou do dispositivo de rede utilizado pelo Usuário para acesso ao Site.
Firewall na VPC – Virtual Private Cloud: sistema que funciona como uma barreira virtual, abrindo e fechando portas de acesso aos aplicativos do Site para a Internet, limitando as oportunidades de invasão.
GDPR – General Data Protection Regulation: norma da União Europeia que regula o tratamento de dados pessoais.
Security Groups: sistema que isola o banco dos Dados de acesso direto à Internet, permitindo que os Dados só sejam acessíveis pelos aplicativos do Site.
SSL – Secure Sockets Layer: tecnologia utilizada para a segurança na comunicação entre o Usuário e o Site.
WAF – Web Application Firewall: camada de segurança que protege de invasores o Site e seus recursos de software.
6. Disposições Gerais
6.1. As comunicações à Bei referidas nesta Política ou relativas ao PQ? devem ser endereçadas à seção ‘Contato’ disponível no Site.
6.2. O tratamento dos Dados poderá ocorrer durante todo o período de atividade do PQ? e de eventual plataforma que venha sucedê-lo.
6.3. Independentemente de aviso, a Bei poderá revelar quaisquer dados relativos ao Usuário, em cumprimento de ordem judicial ou de outra autoridade competente, ou dever legal.
6.4. Esta Política está disponível no Site e foi registrada no 9º Oficial de Registro de Títulos e Documentos e Civil de Pessoa Jurídica da Comarca de São Paulo - SP, sob o número 1.350.502.
• • •
1. Vinculação
1.1. Ao acessar ou usar o website do “Por Quê?” (“PQ?” ou “Site”), incluindo os conteúdos e aplicativos disponíveis no Site e em outros domínios utilizados para operar o PQ?, aquele que acessa ou utiliza o Site (“Usuário”) declara ter lido e compreendido estes Termos de Uso (“Termos”), bem como concordado integral e expressamente com os mesmos e estar obrigado a cumprir irrestritamente as condições aqui estabelecidas, formando um contrato entre o Usuário e a Bei Comunicação Ltda. (“Bei”).
1.2. O Usuário declara ser maior de idade e capaz, tendo plenas condições para aderir e se vincular às condições destes Termos.
1.3. Caso o Usuário não compreenda ou não concorde com qualquer dispositivo destes Termos (integral ou parcialmente) ou não tenha capacidade legal para contratar, em nome próprio, o Usuário deverá imediatamente deixar o PQ?, fechar a aba ou janela do navegador de Internet que estiver usando para acessá-lo e abster-se de acessar ou de usar, de qualquer forma, o PQ?.
1.4. O Usuário reconhece e concorda que todos os avisos, regulamentos de uso, políticas e instruções apresentados no PQ?, especialmente a Política de Privacidade, integram estes Termos, como se nele estivessem transcritos.
1.5. A Bei pode modificar estes Termos a qualquer tempo, e o Usuário, ao acessar e/ou usar o PQ?, manifestará o seu consentimento e total concordância em cumprir com tais modificações ou revisões. O Usuário deve reler periodicamente a versão vigente deste instrumento (disponível na URL http://www.porque.com.br/), ainda que a Bei procure sempre mantê-lo informado de mudanças importantes realizadas nestes Termos.
1.6. O presente Termo entrará em vigor no momento do primeiro acesso ou utilização do PQ? pelo Usuário e permanecerá em vigor durante o período necessário ao cumprimento integrado destes Termos.
2. Conta no PQ?
2.1. O disposto nesta cláusula 2 será aplicável caso o PQ? disponibilize para Usuários uma conta para o acesso a área restrita ou para certas funcionalidades do Site.
2.2. O Usuário poderá criar uma conta para ter uma experiência mais personalizada no Site. As credenciais de acesso, incluindo o login e sua senha, são pessoais e intransferíveis.
2.3. Ao criar uma conta, o Usuário declara que as informações prestadas são corretas, completas, atuais e verídicas. É de responsabilidade do Usuário a manutenção das informações pessoais atualizadas, corretas, completas e verídicas no banco de dados da Bei.
2.4. O Usuário é o único responsável pela atividade que ocorre em sua conta e deve guardar suas credenciais de acesso em local seguro, sendo o Usuário o único responsável por sua confidencialidade. O Usuário deve notificar imediatamente a Bei sobre qualquer possível violação de segurança ou uso não autorizado de sua conta, ficando responsável pelos atos através dela realizados, até a sua correta comunicação à Bei.
2.5. O Usuário concorda que a Bei, a seu critério exclusivo, poderá cancelar ou suspender sua conta ou parte das funcionalidades a ela relacionadas, sem prévia comunicação:
(a) por descontinuação ou modificação do Site ou de qualquer de suas partes;
(b) por caso fortuito ou força maior;
(c) por questões de segurança;
(d) em função de ordem judicial ou requisição legal de autoridade competente;
(e) caso o Usuário descumpra ou aja de forma que claramente mostre que não pretende ou não pode cumprir qualquer condição destes Termos, demais regulamentos aplicáveis ao PQ? ou legislação vigente; e
(f) caso o Usuário encerre sua relação com a Bei ou este queira excluir sua conta, devendo notificar previamente a Bei, a qualquer momento.
2.6. A decisão de readmissão do Usuário representará mero ato de liberalidade da Bei, não representando, em nenhuma hipótese, qualquer alteração do disposto nestes Termos. Da mesma forma, a readmissão do Usuário não representará a concordância da Bei com a ação ou omissão que resultou no desligamento do Usuário, remanescendo todas as obrigações do Usuário referentes ao uso da conta do Site.
3. Uso do PQ?
3.1. A Bei concede permissão pessoal, não exclusiva e intransferível ao Usuário para este acessar e usar o PQ? de forma lícita, tendo acesso a todo o acervo de imagens, ilustrações, áudios, audiovisuais, textos, aplicativos, bases de dados e outros materiais disponíveis no PQ? (“Conteúdos”). Em contrapartida, o Usuário se compromete a não:
(a) reproduzir ou de qualquer forma copiar, transmitir, explorar ou distribuir os Conteúdos do PQ?, no todo ou em parte, para qualquer finalidade (incluindo texto, imagens e outros materiais), sem a autorização prévia e por escrito da Bei;
(b) alterar ou modificar qualquer parte do PQ? ou qualquer dos Conteúdos;
(c) acessar os Conteúdos através de qualquer tecnologia que não as páginas de exibição do próprio PQ? ou outro meio autorizado pela Bei;
(d) realizar ou participar de qualquer atividade que interfira ou interrompa o funcionamento do Site ou dos equipamentos, programas de computador e/ou serviços a que o PQ? esteja conectado;
(e) carregar, transmitir, divulgar, exibir, enviar ou de qualquer forma tornar disponível qualquer tipo de mensagem, anúncio, propaganda ou material promocional não autorizado previamente pela Bei, por escrito, ou mensagens não solicitadas (conhecidos como "junk mail" ou "spam"), correntes, esquemas de pirâmide ou outras;
(f) usar qualquer sistema automatizado, inclusive, mas sem se limitar a "robôs", que acessem o PQ? de maneira a enviar mais solicitações de acesso ou uso em um dado período do que seja humanamente possível responder no mesmo lapso temporal. O Usuário concorda em não coletar qualquer Conteúdo ou informação que identifique qualquer pessoa, inclusive nomes, credenciais de contas, ou outros dados pessoais, a partir do Site;
(g) agir de forma a prejudicar a Bei ou terceiros;
(h) utilizar o PQ? para qualquer fim outro que o acesso privado e informativo do Site, nem abordar outro usuário do PQ? com qualquer finalidade comercial;
(i) decodificar, descompilar ou efetuar engenharia reversa, para obter códigos fonte, informações e/ou outras características do PQ? e/ou dos Conteúdos;
(j) praticar qualquer ato que possa expor terceiros de modo pejorativo, criar ou compartilhar um conteúdo (i) falso, ilegal, abusivo, que incite a violência, crime ou prática que possa afetar a saúde ou a segurança de pessoas, ou (ii) de caráter difamatório, racista, homofóbico, obsceno, pornográfico, imoral, político, partidário ou comercial, ou (iii) que possa violar a moral, a ética, os bons costumes ou direitos da Bei ou de terceiros;
(k) cumprir com estes Termos, Política de Privacidade e todas as leis e regulamentos aplicáveis, sejam regionais, nacionais ou internacionais.
3.2. A Bei se reserva o direito de suspender, cancelar ou descontinuar qualquer Conteúdo, aplicativo ou acesso do PQ? a qualquer tempo, sem necessidade de prévia informação a quem quer que seja.
3.3. Os links a websites externos que forem eventualmente citados no PQ? não representam qualquer tipo de endosso a esses websites externos nem ao seu conteúdo pela Bei. Qualquer acesso ou uso desses websites externos pelo Usuário será feito por sua própria conta e risco. A Bei também não se responsabiliza caso o endereço do PQ? esteja disponível em outros websites.
3.4. Além das restrições gerais acima expostas, as seguintes condições se aplicam especificamente ao uso dos Conteúdos:
(a) os Conteúdos do PQ? e as marcas ali contidas são de propriedade exclusiva da Bei ou de seus patrocinadores, fornecedores, parceiros ou clientes, conforme o caso, e estão sujeitos às normas de proteção de propriedade intelectual;
(b) os Conteúdos do PQ? são disponibilizados no estado em que se encontram (‘as is’) apenas para informação e uso pessoal do Usuário, sem qualquer tipo de garantia, sendo vedada qualquer cópia, comercialização, licenciamento, distribuição ou qualquer outra forma de exploração para qualquer que seja a finalidade, sem o consentimento prévio e por escrito da Bei;
(c) o Usuário concorda em não violar, desativar ou de qualquer forma interferir em características relacionadas à segurança (incluindo analisar ou testar a vulnerabilidade de qualquer um dos sistemas técnicos ou redes do PQ?) e/ou funcionamento do Site ou características que evitem ou restrinjam o seu uso ou ainda qualquer ato que imponha limitações sobre o uso do PQ? ou de seu Conteúdo;
(d) o Usuário respeitará direitos de propriedade intelectual, segredos de negócio ou quaisquer outros direitos da Bei e/ou de terceiros disponíveis no Site;
(e) o Usuário reconhece que a Bei poderá estabelecer, a seu exclusivo critério, práticas gerais e limites relativos à utilização do Site, os quais deverão ser respeitados pelo Usuário.
3.5. O Usuário reconhece que o Conteúdo do PQ? poderá ser objeto de buscas por ferramentas externas com o único objetivo de criar e disponibilizar ao público correspondência entre o Site, seu Conteúdo e os termos pesquisados. A Bei se reserva o direito de revogar as permissões às ferramentas externas de buscas tanto de forma geral como em casos específicos.
3.6. Caso a Bei disponibilize no PQ? Conteúdos com a opção de download ou impressão, tais Conteúdos poderão ser usados unicamente pelo Usuário, a título não exclusivo, intransferível, apenas para sua referência e sem qualquer conotação comercial, ficando vedada qualquer reprodução, distribuição, transmissão, exibição, licenciamento ou qualquer outra forma de transferência, uso ou exploração, no todo ou em parte, desses Conteúdos, sem o consentimento prévio e por escrito da Bei.
4. Manifestações do Usuário
4.1. Aplica-se o disposto nesta seção a eventuais conteúdos, perguntas, comentários ou outras manifestações (“Manifestações) que o Usuário eventualmente compartilhe com o PQ? ou publique no Site.
4.2. O Usuário será integralmente responsável pelas Manifestações que compartilhar ou publicar, em seu teor, substância, veracidade e demais aspectos, assim como na conformidade dessas Manifestações com o disposto nestes Termos, ficando a Bei e o PQ? isentos de qualquer responsabilidade.
4.3. Ao compartilhar ou publicar uma Manifestação, o Usuário (a) declara e garante expressamente que é o único titular de todos os direitos de autor, de imagem, de privacidade ou de qualquer outra ordem sobre a Manifestação; e (b) licencia à Bei a Manifestação, a título gratuito, irrevogável, irretratável, por todo o período de proteção legal dos direitos incorporados na Manifestação, para o território do Brasil e o exterior, podendo a Bei utilizar, publicar, distribuir, traduzir e disponibilizar tal Manifestação no PQ?, nas redes sociais e outros canais utilizados pelo PQ?, em meio impresso, inclusive mas não se limitando a livros e periódicos, ou qualquer suporte que permita a reprodução da Manifestação, existente ou que venha a ser futuramente criado, sem restrição quanto ao número de reproduções, veículos, suporte de fixação, prazo, território e forma de exploração.
4.4. Como consequência do disposto na cláusula anterior, as visualizações da Manifestação no PQ? poderão ser medidas e computadas em favor do Site.
4.5. O Usuário declara e reconhece que a publicação ou compartilhamento de qualquer Manifestação poderá ensejar seu uso indevido por terceiros, sem qualquer autorização da Bei, sendo a publicação ou compartilhamento por conta e risco exclusivos do Usuário, sem que a Bei tenha qualquer responsabilidade.
4.6. Caso a Manifestação seja publicada no PQ? ou em suas redes sociais ou canais de comunicação, a Bei atribuirá os respectivos créditos na forma em que forem fornecidos pelo Usuário.
4.7. O PQ? poderá, a seu critério exclusivo, excluir qualquer Manifestação, independentemente de prévio aviso ao Usuário e sem que caiba ao Usuário qualquer direito a indenização, resposta, nova manifestação ou qualquer contrapartida em virtude da exclusão da Manifestação.
5. Notificação de Violação de Direitos
5.1. Em caso de violação qualquer regulamento aplicável ao PQ? ou caso o Usuário suspeite de uma violação de direitos ou conteúdo impróprio como, por exemplo, mas sem se limitar, violação a direitos autorais, material obsceno, apologia ao ódio, imagens chocantes e repugnantes, atos perigosos e ilegais ou material difamatório, o Usuário deverá imediatamente notificar a Bei para análise e possível retirada do conteúdo supostamente irregular. Para tanto, o Usuário ou terceiro devidamente identificado deverá enviar um comunicado por escrito, contendo, ao menos, os seguintes dados:
(a) informação do conteúdo em questão e da URL completa da página de reprodução;
(b) declaração informando qual foi a violação identificada no conteúdo apontado pelo Usuário; e
(c) identificação dos detalhes da obra cujos direitos estão sendo violados ou são de propriedade do Usuário ou de terceiros (se essas informações estiverem disponíveis na Internet, recomenda-se que o link de acesso a elas seja enviado juntamente), quando aplicável.
5.2. É necessária a identificação do Usuário declarante, por meio de seu nome completo e demais dados pessoais para contato.
5.3. Qualquer pessoa que intencionalmente apresentar declaração falsa ou incorreta sobre um Conteúdo estará sujeita às punições legalmente aplicáveis, podendo ainda ter seu acesso ao PQ? bloqueado, suspenso ou descontinuado.
6. Responsabilidades e Garantias
6.1. O Usuário concorda que o uso do PQ? se fará exclusivamente para fins educacionais, por sua conta e risco, sendo que a Bei, seus sócios, patrocinadores, parceiros, executivos, profissionais e representantes não terão qualquer responsabilidade perante o Usuário, relacionada ao uso (e suas consequências) do PQ? e/ou do Conteúdo, incluindo qualquer indenização ou outra obrigação, presente ou futura, com relação ao Usuário ou terceiros.
6.2. A Bei não garante a disponibilidade, continuidade ou infalibilidade do PQ? e/ou de seus Conteúdos, nem que esses estejam isentos de falhas, erros, imprecisões. O PQ? e seu Conteúdo são disponibilizados para fins de informação, não apresentando qualquer garantia ou promessa, implícita ou explícita, de desempenho, ou mesmo de estimativa de sucesso ou correção. Ademais, o Usuário está ciente de que ao usar o Site poderá estar exposto a conteúdo que seja impreciso ou ofensivo, apesar de todos os esforços da Bei em sentido contrário.
6.3. O Usuário declara e reconhece que a Bei, seus sócios, patrocinadores, parceiros, executivos, profissionais e representantes não serão responsabilizados por qualquer dano direto, indireto, incidental, especial, punitivo ou imprevisto resultante de quaisquer (i) erros, equívocos ou imprecisão de Conteúdo, (ii) danos pessoais ou materiais, de qualquer natureza, resultante do acesso do Usuário ao PQ?, (iii) qualquer acesso ou uso dos recursos do Site que não tenha sido autorizado pela Bei, (iv) qualquer interrupção ou cessação de transmissão de dados do e para o PQ?, (iv) qualquer bug, vírus, cavalos de Tróia ou malwares que possam ser transmitidos para ou através do PQ? por quaisquer terceiros, e/ou (v) quaisquer erros ou omissões em qualquer Conteúdo ou qualquer perda ou dano de qualquer natureza sofrido em consequência do uso de qualquer Conteúdo ou canal de comunicação do PQ?. As limitações de responsabilidade desta cláusula serão aplicadas na medida máxima permitida por lei na jurisdição competente.
6.4. Sem limitar a generalidade do acima previsto, o Usuário declara estar ciente e concordar que (a) a Bei não controla nem terá qualquer responsabilidade pelo uso de eventuais websites, redes sociais ou outros veículos de comunicação cujos links eventualmente estejam postados no Site, sendo tal uso por sua conta e risco; e (b) nem a Bei nem o PQ? serão responsabilizados por material ou pela conduta difamatória, ofensiva ou ilegal de quaisquer terceiros que estejam usando o PQ? e/ou o Conteúdo.
6.5. O Usuário concorda em defender, indenizar e isentar a Bei, seus sócios, patrocinadores, parceiros, executivos, profissionais, representantes e terceiros de toda e qualquer ação judicial ou procedimento administrativo, com objetivo de obter satisfação quanto a danos, obrigações, perdas, custos ou dívidas (inclusive, mas sem se limitar a honorários advocatícios) oriundos de: (a) uso ou acesso indevido ao PQ? e/ou ao Conteúdo; (b) violação de qualquer cláusula destes Termos, dos demais regulamentos aplicáveis ao PQ? ou da legislação vigente; (c) violação de qualquer direito de terceiros, inclusive, mas sem se limitar a direitos de propriedade intelectual ou de privacidade; ou (d) qualquer alegação de que algum ato praticado pelo Usuário tenha causado perdas ou danos a terceiros. Esta obrigação subsistirá ao término de vigência de estes Termos e ao uso do Site.
6.6. A Bei não presta qualquer garantia expressa, implícita ou de qualquer outra natureza, e não será responsável pela utilidade e adequação do PQ? a qualquer propósito ou necessidade específica do Usuário ou de terceiros. O PQ? tem por finalidade ampliar os conhecimentos de economia e finanças de seus Usuários, não fornecendo informações sobre investimentos específicos, nem consultoria em economia ou finanças.
7. Disposições Gerais
7.1. As comunicações à Bei referidas nestes Termos ou relativas ao PQ? devem ser endereçadas à seção ‘Contato’ disponível no Site.
7.2. Independentemente de aviso, a Bei poderá revelar quaisquer dados relativos ao Usuário e eventual Manifestação a autoridades públicas, em cumprimento de ordem judicial ou de outra autoridade competente, ou dever legal.
7.3. Estes Termos e quaisquer direitos limitados ao uso do Conteúdo concedidos de acordo com o presente não podem ser transferidos ou cedidos pelo Usuário, mas podem ser transferidos, cedidos ou revogados pela Bei, sem qualquer restrição.
7.4. Os nomes, slogans, nomes de domínio e/ou as marcas da Bei e de seus patrocinadores e parceiros não podem ser utilizados pelo Usuário, sendo ainda vedada qualquer alteração, inserção ou modificação nestes identificadores.
7.5. Se qualquer cláusula destes Termos for considerada inválida ou ineficaz por autoridade competente, a invalidade ou ineficácia de tal cláusula não afetará a validade ou eficácia das cláusulas restantes, que permanecerão integralmente válidas e produzindo plenos efeitos.
7.6. Qualquer renúncia ao exercício de direitos decorrentes destes Termos, não será considerada novação, renúncia adicional ou contínua a esse ou a qualquer outro direito, e a omissão por parte da Bei de não fazer valer qualquer direito ou cláusula destes Termos não constituirá renúncia ou novação de tal direito ou cláusula.
7.7. Na hipótese de conflito entre estes Termos e a Política de Privacidade do PQ?, prevalecerá o disposto na Política de Privacidade. Caso haja conflito entre o disposto nestes Termos e qualquer outro regulamento, aviso, política ou regramento deste Site, prevalecerá o disposto nestes Termos.
7.8. Estes Termos e as relações existentes entre o Usuário e a Bei serão regidos pelas leis da República Federativa do Brasil, sem consideração a qualquer disposição sobre conflito de leis.
7.9. O Usuário concorda que: (i) a sede do PQ? será considerada exclusivamente a da Bei, localizada na cidade de São Paulo - SP, Brasil; e (ii) o Usuário concorda que fica eleito o foro da Comarca de São Paulo – SP, Brasil, para dirimir quaisquer dúvidas ou questões oriundas destes Termos, renunciando a qualquer outro, por mais privilegiado que seja.
7.10. Estes Termos estão disponíveis no Site e foram registrados no 9º Oficial de Registro de Títulos e Documentos e Civil de Pessoa Jurídica da Comarca de São Paulo - SP, sob o número 1.350.501.
• • •
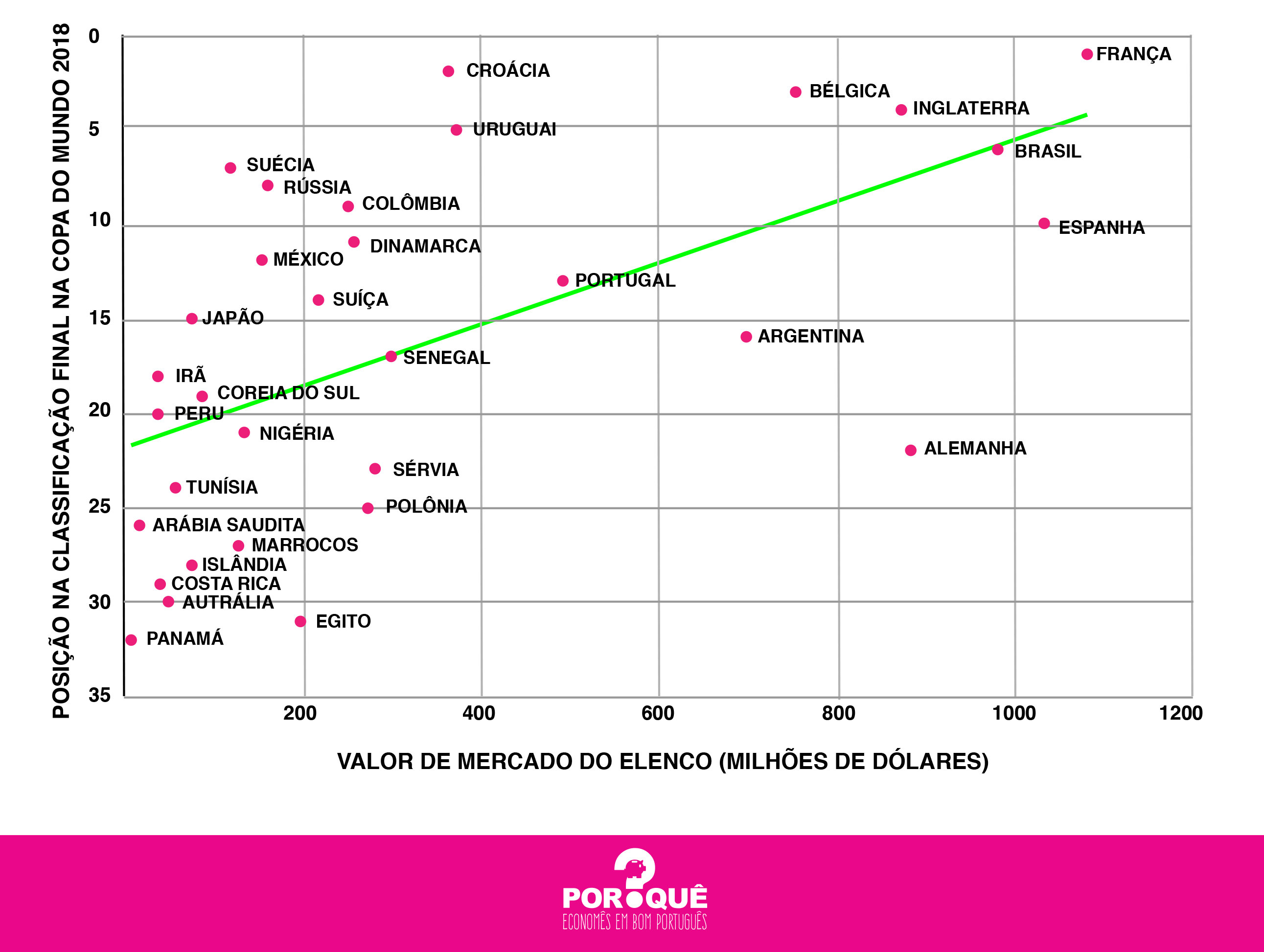A linha verde é a reta que melhor se ajusta aos dados. Note que ela é ascendente, o que significa que há uma correlação positiva entre as variáveis. Seleções mais caras apresentaram, em média, melhor desempenho. Claro que a relação não é perfeita. Note a Croácia, por exemplo, bem acima da reta – seu desempenho é muito melhor do que o previsto pelos dados de valor de mercado. E a Alemanha, bem abaixo. Mas a correlação é relativamente forte (ou seja, o ajuste da reta à nuvem de pontos não é ruim).
O coeficiente de correlação é um índice que mede o grau de associação linear entre duas variáveis. Ele é um número entre -1 e 1. Quanto mais próximo de 1, mais juntamente tendem a andar as duas variáveis. Se ele está próximo de -1, elas também andam juntas, mas em sentido contrário (quando uma sobe, a outra tende a descer).
No gráfico acima, o coeficiente de correlação é aproximadamente 0,6.
Uma curiosidade com relação a esses dados: a seleção mais cara é a França (justamente a campeã), e a mais barata a do Panamá (última colocada).
Calculamos correlações do desempenho com outras duas variáveis: a altura média e a idade média dos jogadores de cada seleção. A seguir exibimos o gráfico do desempenho contra a altura média (em centímetros). A linha de tendência é ascendente, mas há muito ruído. Ela explica muito pouco da variação nos dados.
De fato, o coeficiente de correlação é bem próximo de zero. Aliás, estatisticamente, nem mesmo é possível distinguir esse valor de zero. Não dá para afirmar, portanto, que seleções mais altas se deram melhor no Mundial.
Finalmente, apresentamos a correlação entre classificação e idade média. Nesse caso a reta de tendência é descendente, ou seja, há correlação negativa entre as duas variáveis. Seleções mais jovens, em média, tiveram desempenho melhor. Essa correlação é mais forte do que a anterior, porém não explica muito da variação nos dados. O coeficiente de correlação estimado é igual a -0,2.
Nos exercícios acima estimamos relações entre duas variáveis. Mas há técnicas que nos permitem levar em conta o efeito conjunto de diversas variáveis sobre o desempenho das seleções. Se relacionarmos a classificação das seleções às três variáveis simultaneamente (valor do elenco, altura média e idade média), a única que se correlaciona com o desempenho das seleções é o valor de mercado dos jogadores. O efeito das outras duas não é diferente de zero, em termos estatísticos.
Fontes dos dados:
Classificação final da Copa do Mundo de 2018
Valor de mercado dos jogadores convocados para as seleções (Os dados foram coletados em 30/6. Hoje os valores já mudaram, provavelmente em função do resultado da Copa)
Altura média
Idade média
Para ficar por dentro do que rola no Por Quê?, clique aqui e assine a nossa Newsletter.
